РңРҫРҙРөлиСҖРҫРІР°РҪРёРө
РҫРұСҠРөРәСӮРҫРІ Рё СҒРёСҒСӮРөРј (РӣРөРәСҶРёСҸ)
РҹРӣРҗРқ
РӣР•РҡРҰРҳРҳ
1. РңРҫРҙРөлиСҖРҫРІР°РҪРёРө
СҒРёСҒСӮРөРј Рё СҒСӮСҖСғРәСӮСғСҖРҪСӢР№ СҒРёРҪСӮРөР· РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёС… РјРҫРҙРөР»РөР№
2. РңР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРө
РҫРҝРёСҒР°РҪРёРө РәРёРҪРөСӮРёРәРё РіРҫРјРҫРіРөРҪРҪСӢС… С…РёРјРёСҮРөСҒРәРёС… СҖРөР°РәСҶРёР№
3. РҹРҫСҒСӮСҖРҫРөРҪРёРө
СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёС… РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёС… РјРҫРҙРөР»РөР№ РјРөСӮРҫРҙРҫРј РјРҪРҫР¶РөСҒСӮРІРөРҪРҪРҫРіРҫВ СҖРөРіСҖРөСҒСҒРёРҫРҪРҪРҫРіРҫ Р°РҪализа
4. РһСҒРҪРҫРІРҪСӢРө
РҝСҖРөРҙСҒСӮавлРөРҪРёСҸ Рҫ СҒРёСҒСӮРөРјРө РІРёР·СғалСҢРҪРҫРіРҫ РјРҫРҙРөлиСҖРҫРІР°РҪРёСҸ (VisSim)
1.
РңРҫРҙРөлиСҖРҫРІР°РҪРёРө СҒРёСҒСӮРөРј Рё СҒСӮСҖСғРәСӮСғСҖРҪСӢР№ СҒРёРҪСӮРөР· РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёС… РјРҫРҙРөР»РөР№
РңСӢ РІСӢСҸСҒРҪили, СҮСӮРҫ РұРҫР»СҢСҲРёРҪСҒСӮРІРҫ СҒРёСҒСӮРөРј
С…Р°СҖР°РәСӮРөСҖРёР·СғРөСӮСҒСҸ СҒР»РҫР¶РҪРҫСҒСӮСҢСҺ Рё, СҮСӮРҫ РҝСҖРё РёСҒСҒР»РөРҙРҫРІР°РҪРёРё СҚСӮРёС… СҒРёСҒСӮРөРј РҪРөРҫРұС…РҫРҙРёРјРҫ
РҝСҖРёРұРөРіР°СӮСҢ Рә РҪРөРәРҫСӮРҫСҖСӢРј СғРҝСҖРҫСүРөРҪРёСҸРј.
РўР°Рә РІРҫСӮ, РјРөСӮРҫРҙРҫР»РҫРіРёРөР№ СғРҝСҖРҫСүРөРҪРёСҸ СҒРёСҒСӮРөРј
Р·Р°РҪРёРјР°РөСӮСҒСҸ СӮР°Рә РҪазСӢРІР°РөРјР°СҸ РҫРұСүР°СҸ СӮРөРҫСҖРёСҸ РјРҫРҙРөлиСҖРҫРІР°РҪРёСҸ, Р° РІСҒСҸРәРҫРө РёСҒСҒР»РөРҙРҫРІР°РҪРёРө
СҒРёСҒСӮРөРјСӢ РҪР°СҮРёРҪР°РөСӮСҒСҸ СҒ РҝРҫСҒСӮСҖРҫРөРҪРёСҸ РөРө РјРҫРҙРөли.
Р’ РҫРұСүРөРј СҒР»СғСҮР°Рө РјРҫРҙРөР»СҢ РөСҒСӮСҢ Р°РҪалРҫРі РҫРұСҠРөРәСӮР°,
СҒРёСҒСӮРөРјСӢ или РҝСҖРҫСҶРөСҒСҒР°.
Р Р°СҒСҒРјРҫСӮСҖРёРј СҒРёСҒСӮРөРјСғ, РҝСҖРөРҙСҒСӮавлРөРҪРҪСғСҺ РҪР° СҖРёСҒ.
1.
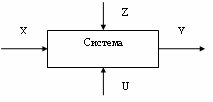
Р РёСҒ.
1.
Р’ СҚСӮРҫР№ СҒРёСҒСӮРөРјРө РҝСҖРҫСҶРөСҒСҒ РјРҫРҙРөлиСҖРҫРІР°РҪРёСҸ
СҒРІРҫРҙРёСӮСҒСҸ Рә РҝРөСҖРөСҖР°РұРҫСӮРәРө РІС…РҫРҙРҪРҫР№ РёРҪС„РҫСҖРјР°СҶРёРё РІ РІС…РҫРҙРҪСғСҺ Рё
СғСҒСӮР°РҪРҫРІР»РөРҪРёСҺ РІРёРҙР° РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ завиСҒРёРјРҫСҒСӮРё РјРөР¶РҙСғ РІСӢС…РҫРҙРҪСӢРјРё Рё РІС…РҫРҙРҪСӢРјРё
РҝР°СҖамРөСӮСҖами СҒРёСҒСӮРөРјСӢ:
Y = F (X, Z, U)В В В В В В В В В В В В В В В В В В В В В В В В В В В В В (1)
Р’ РҫРұСүРөРј СҒР»СғСҮР°Рө РІРёРҙ С„СғРҪРәСҶРёРё (5.1) (или
РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ РјРҫРҙРөли) РјРҫР¶РҪРҫ СӮСҖР°РәСӮРҫРІР°СӮСҢ РәР°Рә С„СғРҪРәСҶРёРҫРҪалСҢРҪСӢР№ РҫРҝРөСҖР°СӮРҫСҖ F, РҫСӮРҫРұСҖажаСҺСүРёР№
С„СғРҪРәСҶРёРҫРҪалСҢРҪРҫРө РҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІРҫ РІС…РҫРҙРҪСӢС… РҝРөСҖРөРјРөРҪРҪСӢС… {Z,U} Рё РҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІРҫ РҝРөСҖРөРјРөРҪРҪСӢС… СҒРҫСҒСӮРҫСҸРҪРёСҸ СҒамРҫР№ СҒРёСҒСӮРөРјСӢ {X} РІ РІ РҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІРҫ РІСӢС…РҫРҙРҪСӢС… РҝРөСҖРөРјРөРҪРҪСӢС… {Y}.
РһРҝРөСҖР°СӮРҫСҖ F РҝСҖРөРҙСҒСӮавлСҸРөСӮ СҒРҫРұРҫР№ замРәРҪСғСӮСғСҺ СҒРёСҒСӮРөРјСғ
РҙиффРөСҖРөРҪСҶиалСҢРҪСӢС…, РёРҪСӮРөРіСҖалСҢРҪСӢС… СғСҖавРҪРөРҪРёР№ Рё СҒРҫРҫСӮРҪРҫСҲРөРҪРёР№ СҚРјРҝРёСҖРёСҮРөСҒРәРҫРіРҫ С…Р°СҖР°РәСӮРөСҖР°,
РҙРҫРҝРҫР»РҪРөРҪРҪСғСҺ РҪРөРҫРұС…РҫРҙРёРјСӢРјРё РҪР°СҮалСҢРҪСӢРјРё Рё РіСҖР°РҪРёСҮРҪСӢРјРё СғСҒР»РҫРІРёСҸРјРё.
РҹРҫР»СғСҮРөРҪРёРө РІРёРҙР° СҚСӮРҫРіРҫ С„СғРҪРәСҶРёРҫРҪалСҢРҪРҫРіРҫ
РҫРҝРөСҖР°СӮРҫСҖа F Рё РұСғРҙРөСӮ РҝРҫРҪРёРјР°СӮСҢСҒСҸ РәР°Рә РҝРҫСҒСӮСҖРҫРөРҪРёРө
РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ РјРҫРҙРөли.
РўР°РәРёРј РҫРұСҖазРҫРј, РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ РјРҫРҙРөР»СҢСҺ
СҒРёСҒСӮРөРјСӢ РҪазСӢРІР°СҺСӮ РөРө РҫРҝРёСҒР°РҪРёРө РҪР° РәР°РәРҫРј лиРұРҫ С„РҫСҖмалСҢРҪРҫРј СҸР·СӢРәРө, РҝРҫР·РІРҫР»СҸСҺСүРөРө РІСӢРҪРҫСҒРёСӮСҢ
СҒСғР¶РҙРөРҪРёСҸ Рҫ РҪРөРәРҫСӮРҫСҖСӢС… СҮРөСҖСӮах РҝРҫРІРөРҙРөРҪРёСҸ СҚСӮРҫР№ СҒРёСҒСӮРөРјСӢ РҝСҖРё РҝСҖРҫРІРөРҙРөРҪРёРё С„РҫСҖмалСҢРҪСӢС…
РҝСҖРҫСҶРөРҙСғСҖ РҪР°Рҙ РөРө РҫРҝРёСҒР°РҪРёРөРј.
В РҡРҫРҪРөСҮРҪРҫР№ СҶРөР»СҢСҺ
СҖазСҖР°РұРҫСӮРәРё РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёС… РјРҫРҙРөР»РөР№ СҸРІР»СҸРөСӮСҒСҸ РҝСҖРҫРіРҪРҫР· СҖРөР·СғР»СҢСӮР°СӮРҫРІ РҝРҫРІРөРҙРөРҪРёСҸ
СҒРёСҒСӮРөРјСӢ (РҝСҖРҫСҶРөСҒСҒР°) Рё РІСӢСҖР°РұРҫСӮРәР° СҖРөРәРҫРјРөРҪРҙР°СҶРёРё РҝРҫ РІРҫР·РјРҫР¶РҪСӢРј РІРҫР·РҙРөР№СҒСӮРІРёСҸС… РҪР° С…РҫРҙ
СҒРёСҒСӮРөРјСӢ или РҝСҖРҫСҶРөСҒСҒР°.
РҹСҖРё РјРҫРҙРөлиСҖРҫРІР°РҪРёРё СҖазлиСҮР°СҺСӮ РҙРІР° РІРёРҙР°
РјРҫРҙРөлиСҖРҫРІР°РҪРёСҸ вҖ“ физиСҮРөСҒРәРҫРө Рё РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРө.В В
РӨРёР·РёСҮРөСҒРәРҫРө РјРҫРҙРөлиСҖРҫРІР°РҪРёРө РҫСҒРҪРҫРІР°РҪРҫ РҪР°
РёСҒРҝРҫР»СҢР·РҫРІР°РҪРёРё РҝСҖРёРҪСҶРёРҝР° РҝРҫРҙРҫРұРёСҸ, СӮР°РәРёС… РәР°Рә
РіРөРҫРјРөСӮСҖРёСҮРөСҒРәРҫРө РҝРҫРҙРҫРұРёРө Рё физиСҮРөСҒРәРҫРө РҝРҫРҙРҫРұРёРө.
РһСҒРҪРҫРІРҪСӢРјРё РІРёРҙами РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёС… РјРҫРҙРөР»РөР№
СҸРІР»СҸСҺСӮСҒСҸ:
1.
РңРҫРҙРөли СҒ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРҪСӢРјРё РҝР°СҖамРөСӮСҖами.
2.
РңРҫРҙРөли СҒ СҒРҫСҒСҖРөРҙРҫСӮРҫСҮРөРҪРҪСӢРјРё РҝР°СҖамРөСӮСҖами.
3.
РЎСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёРө РјРҫРҙРөли.
4.
ДиРҪамиСҮРөСҒРәРёРө РјРҫРҙРөли.
Р•СҒли РҫСҒРҪРҫРІРҪСӢРө РҝРөСҖРөРјРөРҪРҪСӢРө СҒРёСҒСӮРөРјСӢ (РҝСҖРҫСҶРөСҒСҒР°) РёР·РјРөРҪСҸРөСӮСҒСҸ РәР°Рә РІРҫ РІСҖРөРјРөРҪРё,
СӮР°Рә Рё РІ РҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІРө, СӮРҫ РјРҫРҙРөли, РҫРҝРёСҒСӢРІР°СҺСүРёРө СӮР°РәРёРө РҝСҖРҫСҶРөСҒСҒСӢ, РҪазСӢРІР°СҺСӮСҒСҸ
РјРҫРҙРөР»СҸРјРё СҒ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРҪСӢРјРё РҝР°СҖамРөСӮСҖами. РһРҪРё РҫРҝРёСҒСӢРІР°СҺСӮСҒСҸ РІ РІРёРҙРө РҙиффРөСҖРөРҪСҶиалСҢРҪСӢС…
СғРҝСҖавлРөРҪРёР№ СҮР°СҒСӮРҪСӢС… РҝСҖРҫРёР·РІРҫРҙРҪСӢС…. (РқР°РҝСҖРёРјРөСҖ, РјРҫРҙРөР»СҢ РёР·РјРөРҪРөРҪРёСҸ РәРҫРҪСҶРөРҪСӮСҖР°СҶРёРё
РІРөСүРөСҒСӮРІР° РІ РҝлавилСҢРҪРҫРј агСҖРөРіР°СӮРө).
Р•СҒли РёР·РјРөРҪРөРҪРёСҸ РҫСҒРҪРҫРІРҪСӢС… РҝРөСҖРөРјРөРҪРҪСӢС… РҝСҖРҫСҶРөСҒСҒ РІ РҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІРө
РҪРө РҝСҖРҫРёСҒС…РҫРҙРёСӮ, СӮРҫ РјРҫРҙРөли, РҫРҝРёСҒСӢРІР°СҺСүРёРө СӮР°РәРёРө РҝСҖРҫСҶРөСҒСҒСӢ, РҪазСӢРІР°СҺСӮСҒСҸ РјРҫРҙРөР»СҸРјРё СҒ
СҒРҫСҒСҖРөРҙРҫСӮРҫСҮРөРҪРҪСӢРјРё РҝР°СҖамРөСӮСҖами.
РЎСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёРө РјРҫРҙРөли РҫРҝРёСҒСӢРІР°СҺСӮ
СҒСӮР°СҶРёРҫРҪР°СҖРҪСӢРө РҝСҖРҫСҶРөСҒСҒСӢ Рё СҒРҫРҫСӮРІРөСӮСҒСӮРІРөРҪРҪРҫ РҪРө СғСҮРёСӮСӢРІР°СҺСӮ РёР·РјРөРҪРөРҪРёСҸ РҝР°СҖамРөСӮСҖРҫРІ РҝСҖРҫСҶРөСҒСҒР°
РІРҫ РІСҖРөРјРөРҪРё.
ДиРҪамиСҮРөСҒРәРёРө РјРҫРҙРөли РІРҫСҒРҝСҖРҫРёР·РІРҫРҙСҸСӮ РҝСҖРҫСҶРөСҒСҒ
С„СғРҪРәСҶРёРҫРҪРёСҖРҫРІР°РҪРёСҸ СҒРёСҒСӮРөРјСӢ (РёР·РјРөРҪРөРҪРёРө РҝРөСҖРөРјРөРҪРҪСӢС… СҒРёСҒСӮРөРјСӢ) Р·Р° СҖСҸРҙ РҝРҫСҒР»РөРҙРҫРІР°СӮРөР»СҢРҪСӢС…
РјРҫРјРөРҪСӮРҫРІ РІСҖРөРјРөРҪРё.
РҹРҫ РІРёРҙСғ Р°РҝСҖРёРҫСҖРҪРҫР№ РёРҪС„РҫСҖРјР°СҶРёРё
РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёРө РјРҫРҙРөли РҝРҫРҙСҖазРҙРөР»СҸСҺСӮСҒСҸ:
РҗРҪалиСӮРёСҮРөСҒРәРёРө РјРҫРҙРөли вҖ“ РҪР° РҫСҒРҪРҫРІРө
РёРјРөСҺСүРёС…СҒСҸ Р·РҪР°РҪРёР№ Рҫ СҒРІРҫР№СҒСӮвах СҒРёСҒСӮРөРјСӢ СҒР»РҫР¶РҪРҫ РҫРҝСҖРөРҙРөлиСӮСҢ СҒСӮСҖСғРәСӮСғСҖСғ РјРҫРҙРөли Рё
СҮРёСҒР»РөРҪРҪСӢРө Р·РҪР°СҮРөРҪРёСҸ РөРө РәРҫСҚффиСҶРёРөРҪСӮРҫРІ.
РӯРәСҒРҝРөСҖРёРјРөРҪСӮалСҢРҪРҫ-Р°РҪалиСӮРёСҮРөСҒРәРёРө вҖ“ РјРҫРҙРөли Сғ
РәРҫСӮРҫСҖСӢС… РҪР° РҫСҒРҪРҫРІР°РҪРёРё Р°РҝСҖРёРҫСҖРҪСӢС… СҒРІРҫР№СҒСӮРІ РјРҫР¶РҪРҫ РҫСҶРөРҪРёСӮСҢ СҒСӮСҖСғРәСӮСғСҖСғ, РҪРҫ РҪРөР»СҢР·СҸ
РҫРҝСҖРөРҙРөлиСӮСҢ СҮРёСҒР»РөРҪРҪСӢРө Р·РҪР°СҮРөРҪРёСҸ РәРҫСҚффиСҶРёРөРҪСӮРҫРІ РјРҫРҙРөли.
РӯРәСҒРҝРөСҖРёРјРөРҪСӮалСҢРҪСӢРө РјРҫРҙРөли вҖ“ Р°РҝСҖРёРҫСҖРҪСӢС…
СҒРІРөРҙРөРҪРёР№ РҫСҮРөРҪСҢ малРҫ Рё РҪРө РҝРҫР·РІРҫР»СҸРөСӮ РҫСҶРөРҪРёСӮСҢ РҪРё СҒСӮСҖСғРәСӮСғСҖСғ, РҪРё СҮРёСҒР»РөРҪРҪСӢРө Р·РҪР°СҮРөРҪРёСҸ
РәРҫСҚффиСҶРёРөРҪСӮРҫРІ.
Р’ завиСҒРёРјРҫСҒСӮРё
РҫСӮ СҒР»РҫР¶РҪРҫСҒСӮРё РҫРұСҠРөРәСӮР°, РөРіРҫ РҝСҖРёСҖРҫРҙСӢ (СҒСӮРҫС…Р°СҒСӮРёСҮРөСҒРәРёР№ РҝСҖРҫСҶРөСҒСҒ, или
РҙРөСӮРөСҖРјРёРҪРёСҖРҫРІР°РҪРҪСӢР№ РҝСҖРҫСҶРөСҒСҒ) СҒРҫРҫСӮРІРөСӮСҒСӮРІРөРҪРҪРҫ РјРҫРҙРөли РҝРҫРҙСҖазРҙРөР»СҸСҺСӮСҒСҸ РҪР°
РҙРөСӮРөСҖРјРёРҪРёСҖРҫРІР°РҪРҪСӢРө Рё СҒСӮРҫС…Р°СҒСӮРёСҮРөСҒРәРёРө РјРҫРҙРөли.
РһРҝСҖРөРҙРөР»РөРҪРёРө
СҒСӮРөРҝРөРҪРё РұлизРҫСҒСӮРё СҖРөалСҢРҪРҫРіРҫ РҫРұСҠРөРәСӮР° Рё РөРіРҫ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ РјРҫРҙРөли РөСҒСӮСҢ РҫСҒРҪРҫРІРҪР°СҸ
Р·Р°РҙР°СҮР° РҝСҖРё РҝРҫСҒСӮСҖРҫРөРҪРёРё РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ РјРҫРҙРөли Рё РІ РҫРұСүРөРј СҒР»СғСҮР°Рө РҪазСӢРІР°РөСӮСҒСҸ Р·Р°РҙР°СҮРөР№
РёРҙРөРҪСӮифиРәР°СҶРёРё РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ РјРҫРҙРөли, СӮ.Рө. РјРҫРҙРөР»СҢ РҙРҫлжРҪР° Р°РҙРөРәРІР°СӮРҪРҫ РҫРҝРёСҒСӢРІР°СӮСҢ
СҖРөалСҢРҪСӢР№ РҝСҖРҫСҶРөСҒСҒ. Р РөализаСҶРёСҸ РҝСҖРҫСҶРөСҒСҒР° РёРҙРөРҪСӮифиРәР°СҶРёРё РҝСҖРөРҙСҒСӮавлРөРҪР° РҪР° СҖРёСҒ.5.2.
РһСҒРҪРҫРІРҪСӢРө СӮСҖРөРұРҫРІР°РҪРёСҸ, РҫРҝСҖРөРҙРөР»СҸСҺСүРёРө
РІСӢРұРҫСҖ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРіРҫ РҫРҝРёСҒР°РҪРёСҸ. РҹРҫСҒСӮСҖРҫРөРҪРёРө РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРіРҫ РҫРҝРёСҒР°РҪРёСҸ Р»СҺРұРҫРіРҫ
РјРөСӮаллСғСҖРіРёСҮРөСҒРәРҫРіРҫ РҝСҖРҫСҶРөСҒСҒР° СҸРІР»СҸРөСӮСҒСҸ СҒР»РҫР¶РҪРҫР№ Р·Р°РҙР°СҮРөР№ Рё РІ СҚСӮРҫРј СҒР»СғСҮР°Рө РҪСғР¶РҪРҫ
СғСҮРёСӮСӢРІР°СӮСҢ СҒР»РөРҙСғСҺСүРёРө фаРәСӮРҫСҖСӢ:
1. РқалиСҮРёРө
РҙРҫСҒСӮР°СӮРҫСҮРҪРҫРіРҫ РҫРұСҠРөРјР° Р°РҝСҖРёРҫСҖРҪСӢС… СҒРІРөРҙРөРҪРёР№ Рҫ физиРәРҫ-С…РёРјРёСҮРөСҒРәРҫРј
Р·Р°РәРҫРҪРҫРјРөСҖРҪРҫСҒСӮСҸС… РҝСҖРҫСҶРөСҒСҒР° (РҫРұСҠРөРәСӮР°), РҝРҫР·РІРҫР»СҸСҺСүРёС… РҫСҶРөРҪРёСӮСҢ СҒСӮСҖСғРәСӮСғСҖСғ РјРҫРҙРөли РҝСҖРҫСҶРөСҒСҒР°.
2. Р’РҫР·РјРҫР¶РҪРҫСҒСӮСҢ
РёСҒСҒР»РөРҙРҫРІР°РҪРёСҸ РҝСҖРҫСҶРөСҒСҒР° РІ СҲРёСҖРҫРәРҫРј РҙРёР°РҝазРҫРҪРө РёР·РјРөРҪРөРҪРёСҸ РҝРөСҖРөРјРөРҪРҪСӢС… РІ С…РҫРҙРө РҝСҖРҫСҶРөСҒСҒР°.
РӯСӮРёРј РҙРІСғРј СӮСҖРөРұРҫРІР°РҪРёСҸРј
С…РҫСҖРҫСҲРҫ СғРҙРҫРІР»РөСӮРІРҫСҖСҸСҺСӮ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёРө РҫРҝРёСҒР°РҪРёСҸ РҝСҖРҫСҶРөСҒСҒРҫРІ РІ РәлаСҒСҒРө
Р°РҪалиСӮРёРәРҫ-СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёС… РјРҫРҙРөР»РөР№.
Р’ СҚСӮРҫРј РәлаСҒСҒРө РјРҫРҙРөР»РөР№
взаимРҫСҒРІСҸР·Рё РҝРөСҖРөРјРөРҪРҪСӢС… РјРҫРҙРөли РҫРҝРёСҒСӢРІР°СҺСӮСҒСҸ СғСҖавРҪРөРҪРёСҸРјРё РјР°СӮРөСҖиалСҢРҪСӢС… Рё СӮРөРҝР»РҫРІСӢС…
РұалаРҪСҒРҫРІ СҒ СғСҮРөСӮРҫРј СҒСӮРөС…РёРҫРјРөСӮСҖРёРё, РіРёРҙСҖРҫРҙРёРҪамиРәРё Рё РәРёРҪРөСӮРёРәРё РҝСҖРҫСҶРөСҒСҒР°.
РҳСҒС…РҫРҙСҸ, РёР· СҒРәазаРҪРҪРҫРіРҫ
РІСӢРұРҫСҖ РјРөСӮРҫРҙРёРәРё СҒСӮСҖСғРәСӮСғСҖСӢ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ РјРҫРҙРөли СҒРІРҫРҙРёСӮСҒСҸ Рә СҒР»РөРҙСғСҺСүРөРјСғ:
1.
РЎРҫСҒСӮавлРөРҪРёРө СҒРҫРҙРөСҖжаСӮРөР»СҢРҪРҫРіРҫ РҫРҝРёСҒР°РҪРёСҸ СӮРөС…РҪРҫР»РҫРіРёСҮРөСҒРәРҫРіРҫ
РҝСҖРҫСҶРөСҒСҒР° РҪР° РҫСҒРҪРҫРІРө физиСҮРөСҒРәРёС… Рё физиРәРҫ-С…РёРјРёСҮРөСҒРәРёС… Р·Р°РәРҫРҪРҫРјРөСҖРҪРҫСҒСӮРөР№, Р°РҪализа
Р°РҝСҖРёРҫСҖРҪРҫР№ РёРҪС„РҫСҖРјР°СҶРёРё Рё РІСӢРұРҫСҖ РҫСҒРҪРҫРІРҪСӢС… СҚР»РөРјРөРҪСӮР°СҖРҪСӢС… Р°РәСӮРҫРІ.
2.
РҹСҖРёРҪСҸСӮРёРө СҖСҸРҙР° РҙРҫРҝСғСүРөРҪРёР№ РҝРҫ РёРҙРөализаСҶРёРё С…Р°СҖР°РәСӮРөСҖР°
РҝСҖРҫСӮРөРәР°РҪРёСҸ РҫСӮРҙРөР»СҢРҪСӢС… СҚР»РөРјРөРҪСӮР°СҖРҪСӢС… СҸРІР»РөРҪРёР№
3.
РқР° РҫСҒРҪРҫРІРө СҒРҫРҙРөСҖжаСӮРөР»СҢРҪРҫРіРҫ РҫРҝРёСҒР°РҪРёСҸ, СҖР°СҒСҮР»РөРҪРөРҪРёРө
РҝСҖРҫСҶРөСҒСҒР° РҪР° СҚР»РөРјРөРҪСӮР°СҖРҪСӢРө Р°РәСӮСӢ Рё СҒРҫСҒСӮавлРөРҪРёРө РҙР»СҸ РәажРҙРҫРіРҫ РёР· РҪРёС… СҒРҫРҫСӮРІРөСӮСҒСӮРІСғСҺСүРөРіРҫ
СғСҖавРҪРөРҪРёСҸ РҝРҫ СӮРөРј или РёРҪСӢРј физиСҮРөСҒРәРёРј, С…РёРјРёСҮРөСҒРәРёРј или РҙСҖСғРіРёРј Р·Р°РәРҫРҪРҫРјРөСҖРҪРҫСҒСӮСҸРј,
РҫСӮСҖажаСҺСүРёРј С…Р°СҖР°РәСӮРөСҖ РҝСҖРҫСӮРөРәР°РҪРёСҸ РҝСҖРҫСҶРөСҒСҒР°.
4.
РЈРІСҸР·РәР° РҝРҫР»СғСҮРөРҪРҪСӢС… РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёС… РҫРҝРёСҒР°РҪРёР№ РҫСӮРҙРөР»СҢРҪСӢС…
Р°РәСӮРҫРІ СҒ СғСҮРөСӮРҫРј взаимРҫСҒРІСҸР·Р°РҪРҪРҫСҒСӮРё СҸРІР»РөРҪРёР№ РҝСҖРҫСҶРөСҒСҒР°.
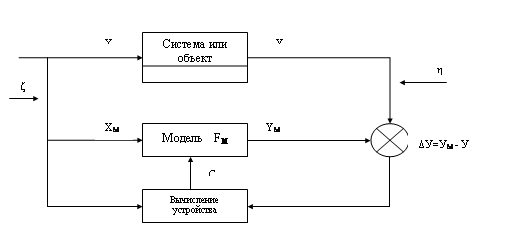
Р РёСҒ. 2.В
БлРҫРә-СҒС…РөРјР° СҖРөализаСҶРёРё РҝСҖРҫСҶРөСҒСҒР° РёРҙРөРҪСӮифиРәР°СҶРёРё
О¶ вҖ“ РҝРҫРјРөС…Р° РҪР°
РІС…РҫРҙРө
О· вҖ“ РҝРҫРјРөС…Р° РҪР°
РІСӢС…РҫРҙРө.
РўРёРҝРҫРІСӢРө РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёРө РјРҫРҙРөли
РҝРҫСӮРҫРәРҫРІ РІ Р°РҝРҝР°СҖР°СӮах (агСҖРөРіР°СӮах). Р’ завиСҒРёРјРҫСҒСӮРё РҫСӮ РІРёРҙР° С„СғРҪРәСҶРёРё
СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ РІСҒРө РјРҪРҫРіРҫРҫРұСҖазиРө РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёС… РјРҫРҙРөР»РөР№ РҝРҫСӮРҫРәРҫРІ, РІРҫР·РҪРёРәР°СҺСүРёС… РІ
СҖазлиСҮРҪСӢС… Р°РҝРҝР°СҖР°СӮах, РјРҫР¶РөСӮ РұСӢСӮСҢ РҝСҖРөРҙСҒСӮавлРөРҪРҫ РІ РІРёРҙРө РҪРөРәРҫСӮРҫСҖСӢС… СӮРёРҝРҫРІСӢС… РјРҫРҙРөР»РөР№.
Рҡ РҪРёРј РҫСӮРҪРҫСҒСҸСӮСҒСҸ:
1. РңРҫРҙРөР»СҢ РёРҙРөалСҢРҪРҫРіРҫ РІСӢСӮРөСҒРҪРөРҪРёСҸ
2. РңРҫРҙРөР»СҢ РёРҙРөалСҢРҪРҫРіРҫ СҒРјРөСҲРөРҪРёСҸ
3. ДиффСғР·РёРҫРҪРҪР°СҸ РјРҫРҙРөР»СҢ
РңРҫРҙРөР»СҢ РёРҙРөалСҢРҪРҫРіРҫ РІСӢСӮРөСҒРҪРөРҪРёСҸ. Р’ СҒРҫРҫСӮРІРөСӮСҒСӮРІРёРё СҒ СҚСӮРҫР№ РјРҫРҙРөР»СҢСҺ
РҝСҖРёРҪРёРјР°РөСӮСҒСҸ РҝРҫСҖСҲРҪРөРІРҫРө СӮРөСҮРөРҪРёРө РҝРҫСӮРҫРәР° РұРөР· РҝРөСҖРөРјРөСҲРёРІР°РҪРёСҸ РҝСҖРё СҖавРҪРҫРјРөСҖРҪРҫРј
СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёРё СҒСғРұСҒСӮР°РҪСҶРёРё (РІРөСүРөСҒСӮРІР°, СҚРҪРөСҖРіРёРё), РҝРөСҖРҝРөРҪРҙРёРәСғР»СҸСҖРҪРҫ РҙРІРёР¶РөРҪРёСҺ (СҖРёСҒ. 3)
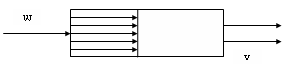
Р РёСҒ.
3. РЎС…РөРјР° РҝРҫСӮРҫРәР°
РңР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРө РҫРҝРёСҒР°РҪРёРө СҒРёСҒСӮРөРјСӢ РёРјРөРөСӮ РІРёРҙ:
![]() В В В В В В В (2),
В В В В В В В (2),
В РіРҙРөВ В В В В
СҒ вҖ“ РәРҫРҪСҶРөРҪСӮСҖР°СҶРёСҸ
РІРөСүРөСҒСӮРІ СҚРҪРөСҖРіРёРё; В П„В вҖ“ РІСҖРөРјСҸ;В
Пү вҖ“ лиРҪРөР№РҪР°СҸ СҒРәРҫСҖРҫСҒСӮСҢ РҝРҫСӮРҫРәР°; С… вҖ“ РәРҫРҫСҖРҙРёРҪР°СӮР°.
РӯСӮРҫР№ РјРҫРҙРөли СҒРҫРҫСӮРІРөСӮСҒСӮРІСғРөСӮ РҝСҖРҫСҶРөСҒСҒСӢ,
РҝСҖРҫРёСҒС…РҫРҙСҸСүРёРө РІ СӮСҖСғРұСҮР°СӮСӢС… Р°РҝРҝР°СҖР°СӮах.
РңРҫРҙРөР»СҢ
РёРҙРөалСҢРҪРҫРіРҫ СҒРјРөСҲРөРҪРёСҸ. РӯСӮР° РјРҫРҙРөР»СҢ
РҫРҝРёСҒСӢРІР°РөСӮ СҖавРҪРҫРјРөСҖРҪРҫРө СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёРө СҒСғРұСҒСӮР°РҪСҶРёРё РІРҫ РІСҒРөРј РҝРҫСӮРҫРәРө (СҖРёСҒ. 4)
В В В
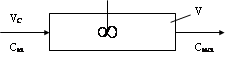
Р РёСҒ.
4. РЎС…РөРјР° РҝРҫСӮРҫРәР°
РңР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРө РҫРҝРёСҒР°РҪРёРө:В В В В В
![]() В В В В В В В В (3)
В В В В В В В В (3)
РһРҝРёСҒСӢРІР°РөСӮ завиСҒРёРјРҫСҒСӮСҢ РјРөР¶РҙСғ РәРҫРҪСҶРөРҪСӮСҖР°СҶРёРөР№
РІРөСүРөСҒСӮРІР° (СҚРҪРөСҖРіРёРё) РІ РҝРҫСӮРҫРәРө РҪР° РІС…РҫРҙРө (РЎРІС…)
Рё РІСӢС…РҫРҙРө (РЎРІСӢС…); V- РҫРұСҠРөРј СҒРёСҒСӮРөРјСӢ; VРЎ -
РҫРұСҠРөРјРҪР°СҸВ СҒРәРҫСҖРҫСҒСӮСҢ РҝРҫСӮРҫРәР°.
РӯСӮРҫР№ РјРҫРҙРөР»СҢСҺ РҫРҝРёСҒСӢРІР°СҺСӮСҒСҸ РҝСҖРҫСҶРөСҒСҒСӢ,
РҝСҖРҫРёСҒС…РҫРҙСҸСүРёРө РІ СҶилиРҪРҙСҖРёСҮРөСҒРәРёС… Р°РҝРҝР°СҖР°СӮах РІ СғСҒР»РҫРІРёСҸС… РёРҪСӮРөРҪСҒРёРІРҪРҫРіРҫ РҝРөСҖРөРјРөСҲРёРІР°РҪРёСҸ.
ДиффСғР·РёРҫРҪРҪР°СҸ РјРҫРҙРөР»СҢ. РӯСӮР°
РјРҫРҙРөР»СҢ РҫРҝРёСҒСӢРІР°РөСӮ РҝСҖРҫСҶРөСҒСҒ РІСӢСӮРөСҒРҪРөРҪРёСҸ, РҫСҒР»РҫР¶РҪРөРҪРҪРҫР№ РҫРұСҖР°СӮРҪСӢРј РҝРөСҖРөРјРөСҲРёРІР°РҪРёРөРј,
С…Р°СҖР°РәСӮРөСҖРёР·СғСҺСүРёРјСҒСҸ С„РҫСҖмалСҢРҪСӢРј Р·Р°РәРҫРҪРҫРј РҙиффСғР·РёРё (СҖРёСҒ.5.5). РҹР°СҖамРөСӮСҖРҫРј,
С…Р°СҖР°РәСӮРөСҖРёР·СғСҺСүРёРј РҙиффСғР·РёРҫРҪРҪСғСҺ РјРҫРҙРөР»СҢ СҸРІР»СҸРөСӮСҒСҸ РәРҫСҚффиСҶРёРөРҪСӮ РҙиффСғР·РёРё DL (или
РәРҫСҚффиСҶРёРөРҪСӮ РҝСҖРҫРҙРҫР»СҢРҪРҫРіРҫ РҝРөСҖРөРјРөСҲРёРІР°РҪРёСҸ).
РҹСҖРё СҒРҫСҒСӮавлРөРҪРёРё СӮР°РәРҫР№ РјРҫРҙРөли РҝСҖРёРҪРёРјР°РөСӮСҒСҸ
СҒР»РөРҙСғСҺСүРёРө РҙРҫРҝСғСүРөРҪРёСҸ:
1. РҳР·РјРөРҪРөРҪРёРө
РәРҫРҪСҶРөРҪСӮСҖР°СҶРёРё СҒСғРұСҒСӮР°РҪСҶРёРё СҸРІР»СҸРөСӮСҒСҸ РҪРөРҝСҖРөСҖСӢРІРҪРҫР№ С„СғРҪРәСҶРёРөР№ РәРҫРҫСҖРҙРёРҪР°СӮСӢ (СҖР°СҒСҒСӮРҫСҸРҪРёСҸ);
2. РҡРҫРҪСҶРөРҪСӮСҖР°СҶРёСҸ
СҒСғРұСҒСӮР°РҪСҶРёРё РІ РҙР°РҪРҪРҫРј СҒРөСҮРөРҪРёРё РҝРҫСҒСӮРҫСҸРҪРҪР°;
3. РһРұСҠРөРјРҪР°СҸ
СҒРәРҫСҖРҫСҒСӮСҢ РҝРҫСӮРҫРәР° Рё РәРҫСҚффиСҶРёРөРҪСӮ DL РҪРө РёР·РјРөРҪСҸСҺСӮСҒСҸ РҝРҫ РҙлиРҪРө Рё СҒРөСҮРөРҪРёСҺ РҝРҫСӮРҫРәР°.
РҹСҖРё СҚСӮРёС… РҙРҫРҝСғСүРөРҪРёСҸС…
РјРҫРҙРөР»СҢ РҫРҝРёСҒСӢРІР°РөСӮСҒСҸ СғСҖавРҪРөРҪРёРөРј: ![]() В В В В В В В В
В В В В В В В В
![]() В - СғСҮРёСӮСӢРІР°РөСӮ
СӮСғСҖРұСғР»РөРҪСӮРҪСғСҺ РҙиффСғР·РёСҺ или РҝРөСҖРөРјРөСҲРёРІР°РҪРёРө. Р’РөлиСҮРёРҪР° DLВ РҫРҝСҖРөРҙРөР»СҸРөСӮСҒСҸ РҫРҝСӢСӮРҪСӢРј РҝСғСӮРөРј.
В - СғСҮРёСӮСӢРІР°РөСӮ
СӮСғСҖРұСғР»РөРҪСӮРҪСғСҺ РҙиффСғР·РёСҺ или РҝРөСҖРөРјРөСҲРёРІР°РҪРёРө. Р’РөлиСҮРёРҪР° DLВ РҫРҝСҖРөРҙРөР»СҸРөСӮСҒСҸ РҫРҝСӢСӮРҪСӢРј РҝСғСӮРөРј.
В В В В В
В В В В В В В В В В В В В В В В В В В В В В
![]()
Р РёСҒ.
5. РЎС…РөРјР° РҝРҫСӮРҫРәР°
2. РңР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРө РҫРҝРёСҒР°РҪРёРө РәРёРҪРөСӮРёРәРё РіРҫРјРҫРіРөРҪРҪСӢС… С…РёРјРёСҮРөСҒРәРёС…
СҖРөР°РәСҶРёР№
РЎСғСүРөСҒСӮРІРөРҪРҪСӢРј РҝСҖРё РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРј РҫРҝРёСҒР°РҪРёРё РіРҫРјРҫРіРөРҪРҪСӢС… С…РёРјРёСҮРөСҒРәРёС… СҖРөР°РәСҶРёРё СҸРІР»СҸРөСӮСҒСҸ РөРө РҝСҖРҫСӮРөРәР°РҪРёРө РІ РҫРҙРҪСғ
СҒСӮР°РҙРёСҺ вҖ“ СҒСӮР°РҙРёСҺ С…РёРјРёСҮРөСҒРәРҫРіРҫ РҝСҖРөРІСҖР°СүРөРҪРёСҸ.
РЎРәРҫСҖРҫСҒСӮСҢСҺ РіРҫРјРҫРіРөРҪРҪРҫР№ С…РёРјРёСҮРөСҒРәРҫР№ СҖРөР°РәСҶРёРё
РҪазСӢРІР°СҺСӮ РёР·РјРөРҪРөРҪРёРө СҮРёСҒла РјРҫР»РөР№ СҖРөагРөРҪСӮРҫРІ РІ РөРҙРёРҪРёСҶСғ РІСҖРөРјРөРҪРё Рё РІ РөРҙРёРҪРёСҶРө РҫРұСҠРөРјР°,
РҝРҫСҚСӮРҫРјСғ РјРҫР¶РҪРҫ Р·Р°РҝРёСҒР°СӮСҢ:
![]() В В В В В В В В В (5)
В В В В В В В В В (5)
mj вҖ“
РҝРҫСҖСҸРҙРҫРә СҒРәРҫСҖРҫСҒСӮРё СҖРөР°РәСҶРёРё РҝРҫ j- РҫРјСғ РІРөСүРөСҒСӮРІСғ. ЧаСҒСӮРҫ m РҝСҖРёРҪРёРјР°СҺСӮ Р·Р° 1 РҙР»СҸ
СғРҝСҖРҫСүРөРҪРёСҸ.
![]() В В В РәРҫРҪСҒСӮР°РҪСӮР° СҒРәРҫСҖРҫСҒСӮРё
С…РёРјРёРјСҮРөСҒРәРҫР№ СҖРөР°РәСҶРёРё
В В В РәРҫРҪСҒСӮР°РҪСӮР° СҒРәРҫСҖРҫСҒСӮРё
С…РёРјРёРјСҮРөСҒРәРҫР№ СҖРөР°РәСҶРёРё
Р• вҖ“ СҚРҪРөСҖРіРёСҸ Р°РәСӮРёРІРҪР°СҸ, СӮ.Рө. СӮР° СҚРҪРөСҖРіРёСҸ РәРҫСӮРҫСҖР°СҸ РҪРөРҫРұС…РҫРҙРёРјР° РҙР»СҸ РҪР°СҮРёРҪР°РҪРёСҸ
РҝСҖРҫС…РҫР¶РҙРөРҪРёСҸ С…РёРјРёСҮРөСҒРәРҫР№ СҖРөР°РәСҶРёРё РјРөР¶РҙСғ СҖРөагРөРҪСӮами
k0 вҖ“ РҝСҖРөРҙСҚРәСҒРҝРҫРҪРөРҪСҶиалСҢРҪСӢР№
РјРҪРҫжиСӮРөР»СҢ
R вҖ“ СғРҪРёРІРөСҖСҒалСҢРҪР°СҸ газРҫРІР°СҸ РҝРҫСҒСӮРҫСҸРҪРҪР°СҸ
Рў вҖ“ СӮРөРјРҝРөСҖР°СӮСғСҖР°
РқР°РҝСҖРёРјРөСҖ: РёРјРөРөРј С…РёРјРёСҮРөСҒРәРёРө СҖРөР°РәСҶРёРё:
![]()
РңР°СӮРөРјР°СӮРёСҮРөСҒРәР°СҸ РјРҫРҙРөР»СҢ РәРёРҪРөСӮРёРәРё СҖРөР°РәСҶРёРё РҝРҫ
РІРөСүРөСҒСӮРІСғ ![]() РұСғРҙРөСӮ РёРјРөСӮСҢ РІРёРҙ:
РұСғРҙРөСӮ РёРјРөСӮСҢ РІРёРҙ:
![]() В (6)
В (6)
В Р’ РҫРұСүРөРј РІРёРҙРө РјРҫР¶РҪРҫ Р·Р°РҝРёСҒР°СӮСҢ, СҮСӮРҫ СҒРәРҫСҖРҫСҒСӮСҢ j вҖ“ РіРҫ РІРөСүРөСҒСӮРІР° РІ СҒРёСҒСӮРөРјРө n вҖ“ С…РёРјРёСҮРөСҒРәРёС… СҖРөР°РәСҶРёРё РұСғРҙРөСӮ
РІСӢРіР»СҸРҙРөСӮСҢ СҒР»РөРҙСғСҺСүРёРј РҫРұСҖазРҫРј:
![]() В В В В В В В В В В В В В В В В В В В В
(7)
В В В В В В В В В В В В В В В В В В В В
(7)
Р•СҒли РҫРұРҫР·РҪР°СҮРёРј Wj
СҒСғРјРјР°СҖРҪСғСҺ СҒРәРҫСҖРҫСҒСӮСҢ РёР·РјРөРҪРөРҪРёСҸ j-РіРҫ
РІРөСүРөСҒСӮРІР° РІ СҒРёСҒСӮРөРјРө СғСҮР°СҒСӮРІСғСҺСүРөРіРҫ РІ n С…РёРјРёСҮРөСҒРәРёС… СҖРөР°РәСҶРёСҸС…, СӮРҫ СҚСӮРҫ РёР·РјРөРҪРөРҪРёРө РјРҫР¶РөСӮ РұСӢСӮСҢ РҫРҝРёСҒР°РҪРҫ
СғСҖавРҪРөРҪРёРөРј РјР°СӮРөСҖиалСҢРҪРҫРіРҫ РұалаРҪСҒР° РІ СҒР»РөРҙСғСҺСүРөРј РІРёРҙРө:
![]() В В В В В В В В В В В В В В В В В В В В В В В
(8)
В В В В В В В В В В В В В В В В В В В В В В В
(8)
РЎСӮРөС…РёРҫРјРөСӮСҖРёСҮРөСҒРәРёР№ РәРҫСҚффиСҶРёРөРҪСӮ РұРөСҖРөСӮСҒСҸ СҒРҫ
Р·РҪР°РәРҫРј В«-В», РөСҒли j-РҫРө РІРөСүРөСҒСӮРІРҫ СҖР°СҒС…РҫРҙСғРөСӮСҒСҸ Рё СҒРҫ Р·РҪР°РәРҫРј
В«+В» РҙР»СҸ РҝСҖРҫРҙСғРәСӮР° СҖРөР°РәСҶРёРё.
РўРҫРіРҙР° СҒ СғСҮРөСӮРҫРј Р·РҪР°СҮРөРҪРёСҸ Vj
РјРҫР¶РҪРҫ Р·Р°РҝРёСҒР°СӮСҢ
![]() В В В В В В В В В В В В В В В В (9)
В В В В В В В В В В В В В В В В (9)
Р“РөСӮРөСҖРҫРіРөРҪРҪСӢРө С…РёРјРёСҮРөСҒРәРёРө СҖРөР°РәСҶРёРё СҸРІР»СҸРөСӮСҒСҸ
РјРҪРҫРіРҫСҒСӮР°РҙРёР№РҪСӢРјРё Рё РІ РҫРұСүРөРј СҒР»СғСҮР°Рө РІРәР»СҺСҮР°РөСӮВ
nВ СҒСӮР°РҙРёР№:
1.
ДиффСғР·РёСҸ газРҫРҫРұСҖазРҪРҫРіРҫ или жиРҙРәРҫРіРҫ РІРөСүРөСҒСӮРІР° Рә Р°РәСӮРёРІРҪРҫР№
РҝРҫРІРөСҖС…РҪРҫСҒСӮРё СҖРөР°РәСҶРёРё
2.
РҗРҙСҒРҫСҖРұСҶРёСҸ РёСҒС…РҫРҙРҪСӢС… СҖРөагРөРҪСӮРҫРІ Рё СҮР°СҒСӮРёСҮРҪР°СҸ РҙРөСҒРҫСҖРұСҶРёСҸ.
3.
РҹРҫРІРөСҖС…РҪРҫСҒСӮРҪР°СҸ С…РёРјРёСҮРөСҒРәР°СҸ СҖРөР°РәСҶРёСҸ СҒ РҫРұСҖазРҫРІР°РҪРёРөРј
газРҫРҫРұСҖазРҪСӢС… или жиРҙРәРёС… РҝСҖРҫРҙСғРәСӮРҫРІ СҖРөР°РәСҶРёРё РІ Р°РҙСҒРҫСҖРұРёСҖРҫРІР°РҪРҪРҫРј СҒРҫСҒСӮРҫСҸРҪРёРё.
4.
Р”РөСҒРҫСҖРұСҶРёСҸ РҝСҖРҫРҙСғРәСӮРҫРІ СҖРөР°РәСҶРёРё СҒ Р°РәСӮРёРІРҪРҫР№ РҝРҫРІРөСҖС…РҪРҫСҒСӮРё.
5.
РһРұСҖР°СӮРҪР°СҸ РҙиффСғР·РёСҸ газРҫРҫРұСҖазРҪСӢС… или жиРҙРәРёС… РҝСҖРҫРҙСғРәСӮРҫРІ
СҖРөР°РәСҶРёРё РІ РҫРұСҠРөРј агСҖРөРіР°СӮР°.
РЎРәРҫСҖРҫСҒСӮСҢ РіРөСӮРөСҖРҫРіРөРҪРҪРҫР№ СҖРөР°РәСҶРёРё СҖавРҪР°
СҒРәРҫСҖРҫСҒСӮРё лимиСӮРёСҖСғСҺСүРөР№ СҒСӮР°РҙРёРё РёВ
РҪРөРҫРұС…РҫРҙРёРјРҫ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРө РҫРҝРёСҒР°РҪРёСҸ РөРө
СҒРҫРҫСӮРІРөСӮСҒСӮРІСғСҺСүРёРј СғСҖавРҪРөРҪРёРөРј.
3. РҹРҫСҒСӮСҖРҫРөРҪРёРө
СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёС… РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёС… РјРҫРҙРөР»РөР№ РјРөСӮРҫРҙРҫРј РјРҪРҫР¶РөСҒСӮРІРөРҪРҪРҫРіРҫВ СҖРөРіСҖРөСҒСҒРёРҫРҪРҪРҫРіРҫ Р°РҪализа
РһРҙРҪРёРј РёР· СҒСҖРөРҙСҒСӮРІ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРіРҫ РҫРҝРёСҒР°РҪРёСҸ
СҒР»РҫР¶РҪРҫРіРҫ РҫРұСҠРөРәСӮР° СҸРІР»СҸРөСӮСҒСҸ СҚРәСҒРҝРөСҖРёРјРөРҪСӮалСҢРҪРҫ-СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёРө РјРөСӮРҫРҙСӢ, РәРҫСӮРҫСҖСӢРө
РҫСҒРҪРҫРІР°РҪСӢ РҪР° РҫРұСҖР°РұРҫСӮРәРө СҚРәСҒРҝРөСҖРёРјРөРҪСӮалСҢРҪРҫРіРҫ РјР°СӮРөСҖиала, СҒРҫРұСҖР°РҪРҪРҫРіРҫ РҪРөРҝРҫСҒСҖРөРҙСҒСӮРІРөРҪРҪРҫ
РҪР° РҙРөР№СҒСӮРІСғСҺСүРөРј РҫРұСҠРөРәСӮРө.
РҹСҖРё СҚСӮРҫРј СҖазлиСҮР°СҺСӮ РҝР°СҒСҒРёРІРҪСӢР№ Рё Р°РәСӮРёРІРҪСӢР№ СҚРәСҒРҝРөСҖРёРјРөРҪСӮ.
РҹР°СҒСҒРёРІРҪСӢР№ СҚРәСҒРҝРөСҖРёРјРөРҪСӮ РҫСҒРҪРҫРІР°РҪ РҪР°
СҖРөРіРёСҒСӮСҖР°СҶРёРё РәРҫРҪСӮСҖРҫлиСҖСғРөРјСӢС… РҝР°СҖамРөСӮСҖРҫРІ РҝСҖРҫСҶРөСҒСҒР° РІ СҖРөжимРө РҪРҫСҖмалСҢРҪРҫРіРҫ
С„СғРҪРәСҶРёРҫРҪРёСҖРҫРІР°РҪРёСҸ РҫРұСҠРөРәСӮР°, РұРөР· РІРҪРөСҒРөРҪРёСҸ РҝСҖРөРҙРҪамРөСҖРөРҪРҪСӢС… РІРҫР·РјСғСүРөРҪРёР№ РҪР° РҫРұСҠРөРәСӮ.
РҗРәСӮРёРІРҪСӢР№ СҚРәСҒРҝРөСҖРёРјРөРҪСӮ РҫСҒРҪРҫРІР°РҪ РҪР°
РёСҒРҝРҫР»СҢР·РҫРІР°РҪРёРё РёСҒРәСғСҒСҒСӮРІРөРҪРҪСӢС… РІРҫР·РјСғСүРөРҪРёР№, РІРІРҫРҙРёРјСӢС… РІ РҫРұСҠРөРәСӮ РҝРҫ Р·Р°СҖР°РҪРөРө
СҒРҝлаРҪРёСҖРҫРІР°РҪРҪРҫР№ РҝСҖРҫРіСҖаммРө.
РҹСҖРё РҫРұСҖР°РұРҫСӮРәРө СҚРәСҒРҝРөСҖРёРјРөРҪСӮалСҢРҪСӢС… РҙР°РҪРҪСӢС…
РёСҒРҝРҫР»СҢР·СғРөСӮСҒСҸ Р°РҝРҝР°СҖР°СӮ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ СҒСӮР°СӮРёСҒСӮРёРәРё, РІРәР»СҺСҮР°СҺСүРёРө СҖазРҙРөР»СӢ
РәРҫСҖСҖРөР»СҸСҶРёРҫРҪРҪРҫРіРҫ СҖРөРіСҖРөСҒСҒРёРҫРҪРҪРҫРіРҫ Рё РҙРёСҒРҝРөСҖСҒРёРҫРҪРҪРҫРіРҫ Р°РҪализа. РҗРҝРҝР°СҖР°СӮ
РәРҫСҖСҖРөР»СҸСҶРёРҫРҪРҪРҫРіРҫ Рё СҖРөРіСҖРөСҒСҒРёРҫРҪРҪРҫРіРҫ Р°РҪализРҫРІ РҝРҫР·РІРҫР»СҸРөСӮ РҝРҫР»СғСҮРёСӮСҢ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРө
РҫРҝРёСҒР°РҪРёРө РҫРұСҠРөРәСӮР° РІ РІРёРҙРө РҝРҫлиРҪРҫРјР° Р·Р°РҙР°РҪРҪРҫРіРҫ РІРёРҙР°, СҒРІСҸР·СӢРІР°СҺСүРөРіРҫ РІС…РҫРҙРҪСӢРө Рё
РІСӢС…РҫРҙРҪСӢРө РҝР°СҖамРөСӮСҖСӢ РҫРұСҠРөРәСӮР°, РәРҫРіРҙР° РҪР° РҫРұСҠРөРәСӮ СҒСғСүРөСҒСӮРІРөРҪРҪСӢРј РҫРұСҖазРҫРј влиСҸСҺСӮ СҒР»СғСҮайРҪСӢРө
фаРәСӮРҫСҖСӢ (СҖРёСҒ. 5.6)
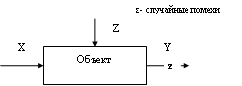
Р РёСҒ.
6
Р’
СӮРөС…РҪРҫР»РҫРіРёСҮРөСҒРәРёС… РҝСҖРҫСҶРөСҒСҒах СҚСӮРё СҒР»СғСҮайРҪСӢРө РҝРҫРјРөС…Рё РІРҫР·РҪРёРәР°СҺСӮ РІСҒР»РөРҙСҒСӮРІРёРө СҖСҸРҙР°
РҝСҖРёСҮРёРҪ:В
1)В В РЎР»СғСҮайРҪСӢРө РҫСҲРёРұРәРё
РёР·РјРөСҖРөРҪРёР№ РІС…РҫРҙРҪСӢС… Рё РІСӢС…РҫРҙРҪСӢС… РҝРөСҖРөРјРөРҪРҪСӢС…;
2) РқРөСғСҮРөСӮ
РҪРөСҒСғСүРөСҒСӮРІРөРҪРҪСӢС…, РҪРҫ РІСҒРө Р¶Рө РҙРөР№СҒСӮРІСғСҺСүРёС… РҪР° РҫРұСҠРөРәСӮ РҝРөСҖРөРјРөРҪРҪСӢС….
Р’ СҚСӮРёС… СғСҒР»РҫРІРёСҸС… Оө вҖ“ С…Р°СҖР°РәСӮРөСҖРёР·СғРөСӮ СҒСғРјРјР°СҖРҪРҫРө РІРҫР·РҙРөР№СҒСӮРІРёРө
СҒР»СғСҮайРҪСӢС… фаРәСӮРҫСҖРҫРІ РҪР° РјРҫРҙРөлиСҖСғРөРјСӢР№ РҫРұСҠРөРәСӮ.
Р Р°СҒСҒРјРҫСӮСҖРёРј завиСҒРёРјРҫСҒСӮСҢ РҪРөРәРҫСӮРҫСҖРҫР№ СҒР»СғСҮайРҪРҫР№
РҝРөСҖРөРјРөРҪРҪРҫР№ YРҫСӮ РҙСҖСғРіРҫР№
СҒР»СғСҮайРҪРҫР№ РҝРөСҖРөРјРөРҪРҪРҫР№ РІРөлиСҮРёРҪСӢ РҘ1.
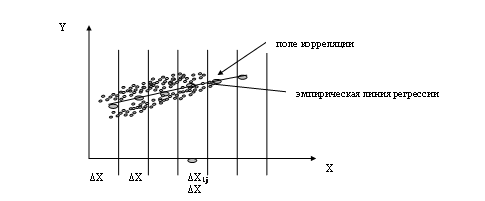
ЗавиСҒРёРјРҫСҒСӮСҢ РјРөР¶РҙСғ РІС…РҫРҙами РҘ1 Рё РІСӢС…РҫРҙами Y РҪР° РҝР»РҫСҒРәРҫСҒСӮРё РҪазСӢРІР°СҺСӮ РҝРҫР»РөРј
РәРҫСҖСҖРөР»СҸСҶРёРё. РҡажРҙРҫРјСғ РҪР°РұР»СҺРҙРөРҪРёСҺ РёР· СӮР°РұлиСҶСӢ РұСғРҙРөСӮ СҒРҫРҫСӮРІРөСӮСҒСӮРІРҫРІР°СӮСҢ РҫРҝСҖРөРҙРөР»РөРҪРҪР°СҸ
СӮРҫСҮРәР° РҪР° РҝРҫР»Рө РәРҫСҖСҖРөР»СҸСҶРёРё.
Р’РөСҒСҢ РҙРёР°РҝазРҫРҪ РёР·РјРөРҪРөРҪРёСҸ РҘ1 СҖазРҫРұСҢРөРј РҪР° СҖСҸРҙ СҖавРҪСӢС… РёРҪСӮРөСҖвалРҫРІ О” РҘ1. В Р’СҒРө СӮРҫСҮРәРё, РҝРҫРҝавСҲРёРө РІ РҙР°РҪРҪСӢР№ РёРҪСӮРөСҖвал РҫСӮРҪРөСҒРөРј Рә СҒРөСҖРөРҙРёРҪРө
СҚСӮРҫРіРҫ РёРҪСӮРөСҖвала РҘ1j. РўРөРҝРөСҖСҢ РҝРҫРҙСҒСҮРёСӮР°РөРј СҮР°СҒСӮРҪСӢРө СҒСҖРөРҙРҪРёРө Р°СҖифмРөСӮРёСҮРөСҒРәРёРө Yj
РҙР»СҸ РәажРҙРҫРіРҫ Р·РҪР°СҮРөРҪРёСҸ
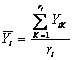 В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В (10)
В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В (10)
РҹСҖРёРјРөСҖ: РҝРҫРҝалРҫ 4 СӮРҫСҮРәРё СҒРҫ Р·РҪР°СҮРөРҪРёСҸРјРё
3,4,2,1;В ![]() ;В В
;В В ![]()
![]() ri вҖ“ СҮРёСҒР»Рҫ
СӮРҫСҮРөРә, РҫРәазавСҲРёС…СҒСҸ РІ РёРҪСӮРөСҖвалРө, РҝСҖРёСҮРөРј -
ri вҖ“ СҮРёСҒР»Рҫ
СӮРҫСҮРөРә, РҫРәазавСҲРёС…СҒСҸ РІ РёРҪСӮРөСҖвалРө, РҝСҖРёСҮРөРј - ![]() , РіРҙРө N
вҖ“ РҫРұСүРөРө СҮРёСҒР»Рҫ РҪР°РұР»СҺРҙРөРҪРёР№.
, РіРҙРө N
вҖ“ РҫРұСүРөРө СҮРёСҒР»Рҫ РҪР°РұР»СҺРҙРөРҪРёР№.
РӯРјРҝРёСҖРёСҮРөСҒРәР°СҸ лиРҪРёСҸ СҖРөРіСҖРөСҒСҒРёРё РҝРҫРәазСӢРІР°РөСӮ,
РәР°Рә РІ СҒСҖРөРҙРҪРөРј РёР·РјРөРҪСҸРөСӮСҒСҸ РІС…РҫРҙРҪР°СҸ РІРөлиСҮРёРҪР° Y СҒ СғРІРөлиСҮРөРҪРёРөРј РҘ1 .
РһСҮРөРІРёРҙРҪРҫ, СҒ СҖРҫСҒСӮРҫРј СҮРёСҒла РҪР°РұР»СҺРҙРөРҪРёР№ лиРҪРёСҸ
СҖРөРіСҖРөСҒСҒРёРё РұСғРҙРөСӮ РҫСҒРІРҫРұРҫР¶РҙР°СӮСҢСҒСҸ РҫСӮ СҒР»СғСҮайРҪСӢС… зигзагРҫРІ, РҝСҖРёРҪРёРјР°СҸ РІСҒРө РұРҫР»РөРө
РҝСҖавилСҢРҪСӢР№ Р·Р°РәРҫРҪРҫРјРөСҖРҪСӢР№ РІРёРҙ. РқахРҫР¶РҙРөРҪРёРө лиРҪРёРё СҖРөРіСҖРөСҒСҒРёРё РҝРҫ СҖРөР·СғР»СҢСӮР°СӮам
РәРҫРҪРөСҮРҪРҫРіРҫ СҮРёСҒла РҪР°РұР»СҺРҙРөРҪРёР№ Рё СҒРҫСҒСӮавлСҸРөСӮ Р·Р°РҙР°СҮСғ РәРҫСҖСҖРөР»СҸСҶРёРҫРҪРҪРҫРіРҫ Р°РҪализа.
РҹРҫ РІРёРҙСғ СҚРјРҝРёСҖРёСҮРөСҒРәРҫР№ лиРҪРёРё СҖРөРіСҖРөСҒСҒРёРёВ РјРҫР¶РҪРҫ РҝРҫРҙРҫРұСҖР°СӮСҢ СғСҖавРҪРөРҪРёРө СҖРөРіСҖРөСҒСҒРёРёВ В
![]() В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В (11)
В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В (11)
Р—Р°РҙР°СҮР° РҫРҝСҖРөРҙРөР»РөРҪРёСҸ РҝР°СҖамРөСӮСҖРҫРІ СғСҖавРҪРөРҪРёСҸ
СҖРөРіСҖРөСҒСҒРёРё СҒРІРҫРҙРёСӮСҒСҸ РҝСҖР°РәСӮРёСҮРөСҒРәРё Рә РҫРҝСҖРөРҙРөР»РөРҪРёСҺ РјРёРҪРёРјСғРјР° С„СғРҪРәСҶРёРё РјРҪРҫРіРёС…
РҝРөСҖРөРјРөРҪРҪСӢС….
![]() В В В В В В В В В В В В В В В В В В (12)
В В В В В В В В В В В В В В В В В В (12)
РҹСҖРҫСҶРөСҒСҒ РҪахРҫР¶РҙРөРҪРёСҸ лиРҪРёРё СҖРөРіСҖРөСҒСҒРёРё (или
СғСҖавРҪРөРҪРёСҸ СҖРөРіСҖРөСҒСҒРёРё) СҒРІРҫРҙРёСӮСҒСҸ Рә СҖР°СҒСҮРөСӮСғ РҝР°СҖамРөСӮСҖРҫРІ ![]() В РөРө СғСҖавРҪРөРҪРёСҸ СҒРҝРҫСҒРҫРұРҫРј
РҪаимРөРҪСҢСҲРёС… РәРІР°РҙСҖР°СӮРҫРІ.
В РөРө СғСҖавРҪРөРҪРёСҸ СҒРҝРҫСҒРҫРұРҫРј
РҪаимРөРҪСҢСҲРёС… РәРІР°РҙСҖР°СӮРҫРІ.
РЎСғСүРҪРҫСҒСӮСҢ СҒРҝРҫСҒРҫРұР° СҒРҫСҒСӮРҫРёСӮ РІ СҒР»РөРҙСғСҺСүРөРј:
Р•СҒли РҙР»СҸ РәажРҙРҫРіРҫ фиРәСҒРёСҖРҫРІР°РҪРҪРҫРіРҫ
Р·РҪР°СҮРөРҪРёСҸВ РҘ1jВ РІРөлиСҮРёРҪР° Y РҪРҫСҖмалСҢРҪРҫ СҖР°СҒРҝСҖРөРҙРөР»РөРҪР°, СӮРҫ РҪаилСғСҮСҲРёРө
РҫСҶРөРҪРәРё РҙР»СҸ РәРҫСҚффиСҶРёРөРҪСӮРҫРІ СғСҖавРҪРөРҪРёСҸ лиРҪРёРё СҖРөРіСҖРөСҒСҒРёРё РҝРҫР»СғСҮР°РөСӮСҒСҸ РҝСҖРё РҙРҫСҒСӮРёР¶РөРҪРёРё
СғСҒР»РҫРІРёСҸ:
![]() В В В В В В (13)
В В В В В В (13)
СӮ.Рө. СҒСғРјРјР° РәРІР°РҙСҖР°СӮРҫРІ РҫСӮРәР»РҫРҪРөРҪРёР№
СҚРәСҒРҝРөСҖРёРјРөРҪСӮалСҢРҪСӢС… Р·РҪР°СҮРөРҪРёР№ YРӯi В РҫСӮ Р·РҪР°СҮРөРҪРёР№ YСҖi СҖР°СҒСҒСҮРёСӮР°РҪРҪСӢС…
РҝРҫ СғСҖавРҪРөРҪРёСҺ Y = Р°0 +Р°1РҘ1 РҙРҫлжРҪР° РұСӢСӮСҢ
РҪаимРөРҪСҢСҲРөР№.
РҳР·Р»РҫР¶РөРҪРҪСӢР№ РҝСҖРёРҪСҶРёРҝ СҒРҝСҖавРөРҙлив Рё СӮРҫРіРҙР°,
РәРҫРіРҙР° РёСҒСҒР»РөРҙСғРөСӮСҒСҸ завиСҒРёРјРҫСҒСӮСҢ РұРҫР»РөРө СҒР»РҫР¶РҪР°СҸ РҫСӮ РҙРІСғС… Рё РұРҫР»РөРө РҝРөСҖРөРјРөРҪРҪСӢС…,
РҪР°РҝСҖРёРјРөСҖ,В В В В В В В В ![]()
Р’ СҚСӮРҫРј СҒР»СғСҮР°Рө СҖР°СҒСҒРјР°СӮСҖРёРІР°РөСӮСҒСҸ,
РјРҪРҫР¶РөСҒСӮРІРөРҪРҪР°СҸ РәРҫСҖСҖРөР»СҸСҶРёСҸ Рё СғР¶Рө СҖР°СҒСҒРјР°СӮСҖРёРІР°СҺСӮ РҪРө лиРҪРёСҺ СҖРөРіСҖРөСҒСҒРёРё, Р°
СҒРҫРҫСӮРІРөСӮСҒСӮРІРөРҪРҪРҫ РҝР»РҫСҒРәРҫСҒСӮСҢ или РіРёРҝРөСҖРҝР»РҫСҒРәРҫСҒСӮСҢ СҖРөРіСҖРөСҒСҒРёРё, Р° СӮРөСҒРҪРҫСӮСғ СҒРІСҸР·Рё РІСӢС…РҫРҙРҪРҫР№
РҝРөСҖРөРјРөРҪРҪРҫР№ Y СҒ
РјРҪРҫР¶РөСҒСӮРІРҫРј РІС…РҫРҙРҪСӢС… РҝРөСҖРөРјРөРҪРҪСӢС…В x1, x2, вҖҰ xnВ СғР¶Рө РҫСҶРөРҪРёРІР°СҺСӮ РәРҫСҚффиСҶРёРөРҪСӮРҫРј РәРҫСҖСҖРөР»СҸСҶРёРё R. Р’РөлиСҮРёРҪР° R РёР·РјРөРҪСҸРөСӮСҒСҸ РІ РҙРёР°РҝазРҫРҪРө ![]() В РөСҒли R=1, СӮРҫ СҒРІСҸР·СҢ С„СғРҪРәСҶРёРҫРҪалСҢРҪР°СҸ, РөСҒли R=0, СӮРҫ РәРҫСҖСҖРөР»СҸСҶРёРҫРҪРҪР°СҸ СҒРІСҸР·СҢ
РҫСӮСҒСғСӮСҒСӮРІСғРөСӮ, РөСҒли 0<R<1,
СӮРҫ РіРҫРІРҫСҖСҸСӮ Рҫ РҪалиСҮРёРё РұРҫР»РөРө или РјРөРҪРөРө СӮРөСҒРҪРҫР№ РәРҫСҖСҖРөР»СҸСҶРёРҫРҪРҪРҫР№ СҒРІСҸР·Рё. РЈСҖавРҪРөРҪРёРө
(5.14) С…Р°СҖР°РәСӮРөСҖРёР·СғРөСӮ РҝРҫР»РҪСғСҺ РәРҫСҖСҖРөР»СҸСҶРёРҫРҪРҪСғСҺ завиСҒРёРјРҫСҒСӮСҢ РјРөР¶РҙСғ РҘ Рё Y.
В РөСҒли R=1, СӮРҫ СҒРІСҸР·СҢ С„СғРҪРәСҶРёРҫРҪалСҢРҪР°СҸ, РөСҒли R=0, СӮРҫ РәРҫСҖСҖРөР»СҸСҶРёРҫРҪРҪР°СҸ СҒРІСҸР·СҢ
РҫСӮСҒСғСӮСҒСӮРІСғРөСӮ, РөСҒли 0<R<1,
СӮРҫ РіРҫРІРҫСҖСҸСӮ Рҫ РҪалиСҮРёРё РұРҫР»РөРө или РјРөРҪРөРө СӮРөСҒРҪРҫР№ РәРҫСҖСҖРөР»СҸСҶРёРҫРҪРҪРҫР№ СҒРІСҸР·Рё. РЈСҖавРҪРөРҪРёРө
(5.14) С…Р°СҖР°РәСӮРөСҖРёР·СғРөСӮ РҝРҫР»РҪСғСҺ РәРҫСҖСҖРөР»СҸСҶРёРҫРҪРҪСғСҺ завиСҒРёРјРҫСҒСӮСҢ РјРөР¶РҙСғ РҘ Рё Y.
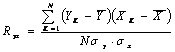 В В В В В В В В В В (14)
В В В В В В В В В В (14)
РіРҙРөВ В
![]() В - Р·РҪР°СҮРөРҪРёРө Рҡ-РіРҫ
Р·РҪР°СҮРөРҪРёСҸ Y
В - Р·РҪР°СҮРөРҪРёРө Рҡ-РіРҫ
Р·РҪР°СҮРөРҪРёСҸ Y
В В В В В В
![]() В В - СҒСҖРөРҙРҪРөРө Р·РҪР°СҮРөРҪРёРө
РҝРөСҖРөРјРөРҪРҪРҫР№ Y
В В - СҒСҖРөРҙРҪРөРө Р·РҪР°СҮРөРҪРёРө
РҝРөСҖРөРјРөРҪРҪРҫР№ Y
В В В В В
![]() В - Рҡ-РҫРө Р·РҪР°СҮРөРҪРёРө РҝРөСҖРөРјРөРҪРҪРҫР№ РҘ
В - Рҡ-РҫРө Р·РҪР°СҮРөРҪРёРө РҝРөСҖРөРјРөРҪРҪРҫР№ РҘ
В В В В
![]() В В - СҒСҖРөРҙРҪРөРө Р·РҪР°СҮРөРҪРёРө
РҝРөСҖРөРјРөРҪРҪРҫР№ РҘ
В В - СҒСҖРөРҙРҪРөРө Р·РҪР°СҮРөРҪРёРө
РҝРөСҖРөРјРөРҪРҪРҫР№ РҘ
В В В В
![]() В В - СҮРёСҒР»Рҫ РҪР°РұР»СҺРҙРөРҪРёР№
В В - СҮРёСҒР»Рҫ РҪР°РұР»СҺРҙРөРҪРёР№
В В В ![]() - СҒСҖРөРҙРҪРөРәРІР°РҙСҖР°СӮРёСҮРҪРҫРө Р·РҪР°СҮРөРҪРёРө СҒРҫРҫСӮРІРөСӮСҒСӮРІСғСҺСүРёС… РҝРөСҖРөРјРөРҪРҪСӢС….
- СҒСҖРөРҙРҪРөРәРІР°РҙСҖР°СӮРёСҮРҪРҫРө Р·РҪР°СҮРөРҪРёРө СҒРҫРҫСӮРІРөСӮСҒСӮРІСғСҺСүРёС… РҝРөСҖРөРјРөРҪРҪСӢС….
РҹСҖРёРјРөСҖ СҖР°СҒСҮРөСӮР° Rxy:
|
РқР°РұР»СҺРҙРөРҪРёСҸ
|
|
|
|
|
|
1 2 3 4 5 |
1 3 5 7 7 |
2 4 6 8 10 |
В В В В В |
В В В В В |
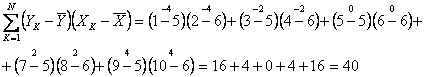

![]()

![]() В В В
В В В ![]()
РңРөСҖРҫР№ СӮРөСҒРҪРҫСӮСӢ СҒРІСҸР·Рё РҙР»СҸ
СҒР»СғСҮР°СҸ РјРҪРҫР¶РөСҒСӮРІРөРҪРҪРҫР№ РәРҫСҖСҖРөР»СҸСҶРёРё СҒР»СғжиСӮ РјРҪРҫР¶РөСҒСӮРІРөРҪРҪСӢР№ РәРҫСҚффиСҶРёРөРҪСӮ РәРҫСҖСҖРөР»СҸСҶРёРё,
РәРҫСӮРҫСҖСӢР№ РјРҫР¶РөСӮ РұСӢСӮСҢ РҫРҝСҖРөРҙРөР»РөРҪ СҮРөСҖРөР· РәРҫСҚффиСҶРёРөРҪСӮСӢ РҝР°СҖРҪРҫР№ РәРҫСҖСҖРөР»СҸСҶРёРё РҝР°СҖамРөСӮСҖРҫРІ,
СғСҮР°СҒСӮРІСғСҺСүРёС… РІ СғСҖавРҪРөРҪРёРё.
В РқР°РҝСҖРёРјРөСҖ, РҙР»СҸ СғСҖавРҪРөРҪРёСҸ СҒ РҙРІСғРјСҸ РҝРөСҖРөРјРөРҪРҪСӢРјРё РҘ1 Рё РҘ2 РәРҫСҚффиСҶРёРөРҪСӮ РјРҪРҫР¶РөСҒСӮРІРөРҪРҪРҫР№
РәРҫСҖСҖРөР»СҸСҶРёРё РҝРҫРҙСҒСҮРёСӮСӢРІР°РөСӮСҒСҸ РҝРҫ С„РҫСҖРјСғР»Рө:
 В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
(15)
В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
(15)
4. РһСҒРҪРҫРІРҪСӢРө
РҝСҖРөРҙСҒСӮавлРөРҪРёСҸ Рҫ СҒРёСҒСӮРөРјРө РІРёР·СғалСҢРҪРҫРіРҫ РјРҫРҙРөлиСҖРҫРІР°РҪРёСҸ (VisSim)
РЎРёСҒСӮРөРјР° РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРіРҫ
РјРҫРҙРөлиСҖРҫРІР°РҪРёСҸВ VisSim РІРөСҖСҒРёРё 4.5,
СҒРҫР·РҙР°РҪРёСҸ фиСҖРјРҫР№ Visual Simulations Incorporating.
РқазваРҪРёРө СҒРёСҒСӮРөРјСӢ РҝСҖРҫРёСҒС…РҫРҙРёСӮ РҫСӮ СҒР»РҫРІВ Visual Simulation вҖ“ РІРёР·СғалСҢРҪР°СҸ
СҒРёРјСғР»СҸСҶРёСҸ. РЈ РҪР°СҒ СҒР»РҫРІРҫ В«СҒРёРјСғР»СҸСҶРёСҸВ» РҙавРҪРҫ РҝСҖРёРҫРұСҖРөР»Рҫ РҪР°СҖРёСҶР°СӮРөР»СҢРҪСӢР№ РҫСӮСӮРөРҪРҫРә,
РҝРҫСҚСӮРҫРјСғ РјСӢ РұСғРҙРөРј РёСҒРҝРҫР»СҢР·РҫРІР°СӮСҢ РұРҫР»РөРө РҝСҖРёРҪСҸСӮСӢР№ Сғ РҪР°СҒ СӮРөСҖРјРёРҪ
«визСғалСҢРҪРҫ-РҫСҖРёРөРҪСӮРёСҖРҫРІР°РҪРҪРҫРө РұР»РҫСҮРҪРҫРө РёРјРёСӮР°СҶРёРҫРҪРҪРҫРө РјРҫРҙРөлиСҖРҫРІР°РҪРёРөВ» или РҙажРө РұРҫР»РөРө
РҝСҖРҫСҒСӮРҫР№ вҖ“ «визСғалСҢРҪРҫРө РјРҫРҙРөлиСҖРҫРІР°РҪРёРөВ».
РһСӮлиСҮРёСӮРөР»СҢРҪР°СҸ РҫСҒРҫРұРөРҪРҪРҫСҒСӮСҢ
СҒРёСҒСӮРөРјСӢ VisSim
вҖ“ РөРө СҸРІРҪР°СҸ РҫСҖРёРөРҪСӮР°СҶРёСҸ РҪР° РҫСӮРәСҖСӢСӮРҫРө РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРө РјРҫРҙРөлиСҖРҫРІР°РҪРёРө. РқР°РұРҫСҖ РұР»РҫРәРҫРІ
РҙР»СҸ РјРҫРҙРөР»РөР№ РІ СҚСӮРҫР№ СҒРёСҒСӮРөРјРө СҖРөР·РәРҫ СҒРҫРәСҖР°СүРөРҪ (РІ СҒСҖавРҪРөРҪРёРё СҒ Simulink) Рё РұРҫР»СҢСҲР°СҸ
СҮР°СҒСӮСҢ РұР»РҫРәРҫРІ РҫСҖРёРөРҪСӮРёСҖРҫРІР°РҪР° РҪР° СҖРөализаСҶРёСҺ РёРјРөРҪРҪРҫ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёС… Рё
Р»РҫРіРёСҮРөСҒРәРёС…В РҫРҝРөСҖР°СҶРёР№. РӯСӮРҫ РҝРҫР·РІРҫР»СҸРөСӮ
СҒРҫР·РҙаваСӮСҢ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёРө РҝСҖРҫР·СҖР°СҮРҪСӢРө РјРҫРҙРөли СҒ Р»СҺРұСӢРјРё
РҫРҝРёСҒСӢРІР°СҺСүРёРјРё РёС… завиСҒРёРјРҫСҒСӮСҸРјРё, РІ СӮРҫРј СҮРёСҒР»Рө СҖРөализРҫРІР°РҪРҪСӢРјРё РІ СҒРёСҒСӮРөмах
РәРҫРјРҝСҢСҺСӮРөСҖРҪРҫР№ РјР°СӮРөРјР°СӮРёРәРё, РҪР°РҝСҖРёРјРөСҖ СӮР°РәРёС… РёР·РІРөСҒСӮРҪСӢС… Рё РҝРҫР»СғСҮРёРІСҲРёС… РјР°СҒСҒРҫРІРҫРө
РҝСҖРёР·РҪР°РҪРёРө, РәР°Рә MathcadВ Рё MATLAB.
ДаРҪРҪР°СҸ РІРөСҖСҒРёСҸ VisSim
РҝРҫСҒСӮавлСҸРөСӮСҒСҸ Рё РёРҪСӮРөРіСҖРёСҖСғРөСӮСҒСҸ СҒ РјР°СҒСҒРҫРІСӢРјРё СҒРёСҒСӮРөмами РәРҫРјРҝСҢСҺСӮРөСҖРҪРҫР№ РјР°СӮРөРјР°СӮРёРәРё Mathcad
2000/2001/2001i/11, РұлагРҫРҙР°СҖСҸ СҮРөРјСғ РҫРҪР° РІРҝРҫР»РҪРө РҙРҫСҒСӮСғРҝРҪР° Рё РёРјРөРөСӮСҒСҸ РҪР° СҖСҸРҙРө
РІСӢРҝСғСүРөРҪРҪСӢС… РІ Р РҫСҒСҒРёРё CD-ROM.
РҳРҪСӮРөРіСҖР°СҶРёСҸ VisSim
4.5 СҒ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёРјРё СҒРёСҒСӮРөмами Mathcad Рё MATLAB РҫСӮРәСҖСӢРІР°РөСӮ РҪРҫРІСӢРө РІРҫР·РјРҫР¶РҪРҫСҒСӮРё
РІСӢРҝРҫР»РҪРөРҪРёСҸ СҒамСӢС… СҒРөСҖСҢРөР·РҪСӢС… РІСӢСҮРёСҒР»РөРҪРёР№, РҝСҖРёСҮРөРј РәР°Рә РІ С…РҫРҙРө РјРҫРҙРөлиСҖРҫРІР°РҪРёСҸ, СӮР°Рә Рё РҝСҖРё
РҫРұСҖР°РұРҫСӮРәРө РөРіРҫ СҖРөР·СғР»СҢСӮР°СӮРҫРІ.
РқазРҪР°СҮРөРҪРёРө Рё СҒРҫСҒСӮав СҒРёСҒСӮРөРјСӢ VisSim
4.5. РЎРёСҒСӮРөРјР° VisSim
(РҙР»СҸ РҫРҝСҖРөРҙРөР»РөРҪРҪРҫСҒСӮРё РҪаиРұРҫР»РөРө СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪРҪР°СҸ РІРөСҖСҒРёСҸ VisSim 4.5)
РҝСҖРөРҙРҪазРҪР°СҮРөРҪР° РҙР»СҸ СҖРөСҲРөРҪРёСҸ Р·Р°РҙР°СҮ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРіРҫ РјРҫРҙРөлиСҖРҫРІР°РҪРёСҸ, РҫСӮРҪРҫСҒСҸСүРёС…СҒСҸ Рә
СҒР»РөРҙСғСҺСүРёРј РәлаСҒСҒам:
В·
лиРҪРөР№РҪСӢРө СҒРёСҒСӮРөРјСӢ;
В·
РҪРөлиРҪРөР№РҪСӢРө СҒРёСҒСӮРөРјСӢ;
В·
РҪРөРҝСҖРөСҖСӢРІРҪСӢРө РІРҫ РІСҖРөРјРөРҪРё СҒРёСҒСӮРөРјСӢ;
В·
РҙРёСҒРәСҖРөСӮРҪСӢРө РІРҫ РІСҖРөРјРөРҪРё СҒРёСҒСӮРөРјСӢ;
В·
СҒРёСҒСӮРөРјСӢ СҒ РёР·РјРөРҪСҸРөРјСӢРјРё РІРҫ РІСҖРөРјРөРҪРё РҝР°СҖамРөСӮСҖами;
В·
РіРёРұСҖРёРҙРҪСӢРө СҒРёСҒСӮРөРјСӢ;
В·
РјРҪРҫРіРҫСҶРөР»РөРІСӢРө Рё РјРҪРҫРіРҫРәРҫРјРҝРҫРҪРөРҪСӮРҪСӢРө СҒРёСҒСӮРөРјСӢ;
В·
РҫРҙРҪРҫРІС…РҫРҙРҫРІСӢРө Рё РҫРҙРҪРҫРІСӢС…РҫРҙРҪСӢРө (РҫРҙРҪРҫРјРөСҖРҪСӢРө) СҒРёСҒСӮРөРјСӢ SISO;
В·
РјРҪРҫРіРҫРІС…РҫРҙРҫРІСӢРө Рё РјРҪРҫРіРҫРІСӢС…РҫРҙРҫРІСӢРө
(РјРҪРҫРіРҫРјРөСҖРҪСӢРө) СҒРёСҒСӮРөРјСӢ MIMO;
В·
РіРёРұСҖРёРҙРҪСӢРө СҒРёСҒСӮРөРјСӢ.
РЎРёСҒСӮРөРјР° VisSim РҪРө РёРјРөРөСӮ СҸРІРҪРҫР№
РҫСҖРёРөРҪСӮР°СҶРёРё РҪР° РәР°РәРҫР№-СӮРҫ РәлаСҒСҒ РјРҫРҙРөлиСҖРҫРІР°РҪРёСҸ. РӯСӮРҫ СғРҪРёРІРөСҖСҒалСҢРҪР°СҸ СҒРёСҒСӮРөРјР°,
РҙРҫРҝСғСҒРәР°СҺСүР°СҸ РҙРҫСҒСӮР°СӮРҫСҮРҪРҫ РҝСҖРҫСҒСӮРҫРө СҖР°СҒСҲРёСҖРөРҪРёРө Рё РҫРұРөСҒРҝРөСҮРёРІР°СҺСүР°СҸ Р»РөРіРәСғСҺ Р°РҙР°РҝСӮР°СҶРёСҺ РҝРҫРҙ
СҖРөСҲРөРҪРёРө СӮРөС… или РёРҪСӢС… РәРҫРҪРәСҖРөСӮРҪСӢС… Р·Р°РҙР°СҮ РҝРҫР»СҢР·РҫРІР°СӮРөР»СҸ. РўРөРј РҪРө РјРөРҪРөРө, СҒСҮРёСӮР°СӮСҢ, СҮСӮРҫ
РҪаиРұРҫР»РөРө СғРҙРҫРұРҪР° РҙР°РҪРҪР°СҸ СҒРёСҒСӮРөРјР° РҙР»СҸ СҖРөСҲРөРҪРёСҸ Р·Р°РҙР°СҮ РІ РҫРұлаСҒСӮРё авСӮРҫРјР°СӮРёСҮРөСҒРәРҫРіРҫ
СҖРөРіСғлиСҖРҫРІР°РҪРёСҸ Рё СғРҝСҖавлРөРҪРёСҸ, Р° СӮР°РәР¶Рө РҝСҖРё РјРҫРҙРөлиСҖРҫРІР°РҪРёРё СҖазлиСҮРҪСӢС… физиСҮРөСҒРәРёС…,
С…РёРјРёСҮРөСҒРәРёС…, СҚРәРҫРҪРҫРјРёСҮРөСҒРәРёС… Рё РҝСҖРҫСҮРёС… СҸРІР»РөРҪРёР№ Рё СҒРёСҒСӮРөРј.
VisSim 4.5 РјРҫР¶РөСӮ СҖР°РұРҫСӮР°СӮСҢ РІ СҒСҖРөРҙРө РҫРҝРөСҖР°СҶРёРҫРҪРҪСӢС… СҒРёСҒСӮРөРј Windows 95/98 NT 4+. Р‘СӢла РҝСҖРҫРІРөРҙРөРҪР°
СҖР°РұРҫСӮРҫСҒРҝРҫСҒРҫРұРҪРҫСҒСӮСҢ СҒРёСҒСӮРөРјСӢ РІ СҒСҖРөРҙРө Windows 2000/РҘР . РқРёРәР°РәРёС… РҫСӮРәР»РҫРҪРөРҪРёР№ РІ СҖР°РұРҫСӮРө СҒРёСҒСӮРөРјСӢ РІСӢСҸРІР»РөРҪРҫ РҪРө
РұСӢР»Рҫ. VisSim
СӮСҖРөРұСғРөСӮ РІРөСҒСҢРјР° СҒРәСҖРҫРјРҪСӢС… Р°РҝРҝР°СҖР°СӮРҪСӢС… СҖРөСҒСғСҖСҒРҫРІ вҖ“ РҹРҡ РҙРҫлжРөРҪ РёРјРөСӮСҢ РҫРҝРөСҖР°СӮРёРІРҪСғСҺ
РҝамСҸСӮСҢ СҒ РјРёРҪималСҢРҪСӢРј РҫРұСҠРөРјРҫРј 4 РңРұ Рё РҫРұСҠРөРјРҫРј СҒРІРҫРұРҫРҙРҪРҫРіРҫ РҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІР° РҪР° Р¶РөСҒСӮРәРҫРј
РҙРёСҒРәРө РҫРәРҫР»Рҫ 30 РңРұ. РһРұСҸР·Р°СӮРөР»СҢРҪРҫ РҪалиСҮРёРө РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРіРҫ СҒРҫРҝСҖРҫСҶРөСҒСҒРҫСҖР°, РҝРҫСҒРәРҫР»СҢРәСғ
РІ С…РҫРҙРө РјРҫРҙРөлиСҖРҫРІР°РҪРёСҸ СҲРёСҖРҫРәРҫ РёСҒРҝРҫР»СҢР·СғРөСӮСҒСҸ 64-РұРёСӮРҪСӢР№ С„РҫСҖРјР°СӮ СҮРёСҒРөР» СҒ РҝлаваСҺСүРөР№
СӮРҫСҮРәРҫР№, РҫРұРөСҒРҝРөСҮРёРІР°СҺСүРёР№ РҫСҮРөРҪСҢ малСӢРө РІСӢСҮРёСҒлиСӮРөР»СҢРҪСӢРө РҝРҫРіСҖРөСҲРҪРҫСҒСӮРё.
ДлСҸ РҝРҫСҒСӮСҖРҫРөРҪРёСҸ РјРҫРҙРөР»РөР№ РІ
СҒРёСҒСӮРөРјРө VisSim
РёСҒРҝРҫР»СҢР·СғСҺСӮСҒСҸ РұР»РҫРәРё, РәРҫСӮРҫСҖСӢРө С…СҖР°РҪСҸСӮСҒСҸ РІ РұРёРұлиРҫСӮРөРәРө РұР»РҫРәРҫРІ Рё РјРҫРіСғСӮ РұСҖР°СӮСҢСҒСҸ РёР·
РҪРөРө, РҝРөСҖРөРҪРҫСҒРёСӮСҢСҒСҸ РІ РҫРәРҪРҫ РјРҫРҙРөли Рё СҒРҫРөРҙРёРҪСҸСӮСҢСҒСҸВ
РҙСҖСғРі СҒ РҙСҖСғРіРҫРј.
БиРұлиРҫСӮРөРәР° РұР»РҫРәРҫРІ,
РҝСҖРөРҙСҒСӮавлРөРҪРҪР°СҸ РІ РҝРҫР·РёСҶРёРё Blocks
(БлРҫРәРё) РјРөРҪСҺ Рё РёРҪСҒСӮСҖСғРјРөРҪСӮалСҢРҪСӢРјРё РҝР°РҪРөР»СҸРјРё, СҒРҫРҙРөСҖжиСӮ СҒР»РөРҙСғСҺСүРёРө В«СӮРҫма»:
В·
Animation
вҖ“ РұР»РҫРәРё СҒРҫР·РҙР°РҪРёСҸ Р°РҪРёРјР°СҶРёРҫРҪРҪСӢС… РәлиРҝРҫРІ;
В·
Annotation
вҖ“ РұР»РҫРәРё СҒРҫР·РҙР°РҪРёСҸ РәРҫРјРјРөРҪСӮР°СҖРёРөРІ Рё РҫРҝСҖРөРҙРөР»РөРҪРёСҸ РҝРөСҖРөРјРөРҪРҪСӢС…;
В·
Arithmetic
вҖ“ РұР»РҫРәРё Р°СҖифмРөСӮРёСҮРөСҒРәРёС… Рё РұлизРәРёС… Рә РҪРёРј РҫРҝРөСҖР°СҶРёР№;
В·
Boolean
вҖ“ РұР»РҫРәРё Р·Р°РҙР°РҪРёСҸ РҫРҝРөСҖР°СҶРёР№ Р‘СғР»РөРІРҫР№ алгРөРұСҖСӢ;
В·
DDE
вҖ“ РұР»РҫРәРё РёРҪСӮРөСҖС„РөР№СҒР°;
В·
Integration
вҖ“ РұР»РҫРәРё Р·Р°РҙР°РҪРёСҸ РҫРҝРөСҖР°СҶРёР№ РёРҪСӮРөРіСҖРёСҖРҫРІР°РҪРёСҸ;
В·
Linear Systems
вҖ“ РұР»РҫРәРё Р·Р°РҙР°РҪРёСҸ РҝР°СҖамРөСӮСҖРҫРІ РҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІР° СҒРҫСҒСӮРҫСҸРҪРёР№ лиРҪРөР№РҪСӢС… СҒРёСҒСӮРөРј Рё РёС…
РҝРөСҖРөРҙР°СӮРҫСҮРҪСӢС… С„СғРҪРәСҶРёР№;
В·
MATLAB Interface
вҖ“ РұР»РҫРәРё РёРҪСӮРөРіСҖР°СҶРёРё СҒ РјР°СӮРөРјР°СӮРёСҮРәРҫР№ СҒРёСҒСӮРөРјРҫР№ MATLAB;
В·
Matrix Operations
вҖ“ РұР»РҫРәРё Р·Р°РҙР°РҪРёСҸ РјР°СӮСҖРёСҮРҪСӢС… РҫРҝРөСҖР°СҶРёР№;
В·
Nonlinear
вҖ“ РұР»РҫРәРё РҪРөлиРҪРөР№РҪСӢС… РҫРҝРөСҖР°СҶРёР№ Рё СҒРҫР·РҙР°РҪРёСҸ РҪРөлиРҪРөР№РҪСӢС… СҒРёСҒСӮРөРј;
В·
Optimization
вҖ“ РұР»РҫРәРё Р·Р°РҙР°РҪРёСҸ РҫРҝРөСҖР°СҶРёР№ РҫРҝСӮРёРјРёР·Р°СҶРёРё;
В·
Random Generator
вҖ“ РұР»РҫРәРё РіРөРҪРөСҖР°СҶРёРё СҒР»СғСҮайРҪСӢС… СҮРёСҒРөР»;
В·
Real Time
вҖ“ РұР»РҫРәРё РҙР»СҸ СҒРёСҒСӮРөРј СҖРөалСҢРҪРҫРіРҫ РІСҖРөРјРөРҪРё;
В·
Signal Consumer
вҖ“ РұР»РҫРәРё СҖРөРіРёСҒСӮСҖР°СҶРёРё, РёРҪРҙРёРәР°СҶРёРё Рё РҝРҫСҒСӮСҖРҫРөРҪРёСҸ РіСҖафиРәРҫРІ СҒРёРіРҪалРҫРІ;
В·
Signal Producer
вҖ“ РұР»РҫРәРё СҒРҫР·РҙР°РҪРёСҸ СҒРёРіРҪалРҫРІ;
В·
Time Delay
вҖ“ РұР»РҫРәРё СҒРҫР·РҙР°РҪРёСҸ РІСҖРөРјРөРҪРҪРҫР№ Р·Р°РҙРөСҖР¶РәРё;
В·
Transcendental
вҖ“ РұР»РҫРәРё Р·Р°РҙР°РҪРёСҸ СӮСҖР°РҪСҒСҶРөРҪРҙРөРҪСӮРҪСӢС… РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёРө С„СғРҪРәСҶРёР№;
В·
General
вҖ“ С„СғРҪРәСҶРёРё РҫРұСүРөРіРҫ С…Р°СҖР°РәСӮРөСҖР°.